GRE
LINKS:
Answers to first group of questions.
Group 2
Group 2
Geometry topics
include:
parallel and perpendicular lines
NEGATIVE POWERS (EXPONENTS)
********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********
*********************************************************
******************************************************
FUNCTION NOTATION
VIDEO TO WATCH
**********
VIDEOS
********************************************************************************
So the picture at the right implies
we can form 120 letter arrangements
of the letters: W,A,G,O,N
AGONW, AGNOW, ANGOW, etc.
AGONW, AGNOW, ANGOW, etc.
Some types of word problems are easily solved using Combinations:
Suppose that you are going to choose a small group of 3 items
from a larger group of 7 items.
You could list all the possible groups, if need be.
But, you can count the number of the possible groups
by just using COMBINATIONS.
7 choose 3 has _35__ possible groups
7! / (3! times 4!) = 35
(7*6*5*4*3*2*1*)
(3*2*1)(4*3*2*1)
Reduce by dividing top
and bottom by (4!)
= (7*6*5)/(3*2*1)
OR
LOOKING at PASCAL's TRIANGLE
See the row with 1, 7, 21, 35, 35, 21, 7, 1?
7 choose NONE has _1_ possible group
7 choose 1 has _7_ possible groups
7 choose 2 has _21_ possible groups
7 choose 3 has _35_ possible groups
7 choose 4 has _35_ possible groups
7 choose 5 has _21_ possible groups
7 choose 6 has _7_ possible groups
7 choose 7 has _1_ possible groups
7 choose NONE has _1_ possible group
7 choose 1 has _7_ possible groups
7 choose 2 has _21_ possible groups
7 choose 3 has _35_ possible groups
7 choose 4 has _35_ possible groups
7 choose 5 has _21_ possible groups
7 choose 6 has _7_ possible groups
7 choose 7 has _1_ possible groups
*************************************
Suppose we wish to arrange n = 5 people {a, b, c, d, e}, standing side by side, for
a portrait. How many such distinct portraits (“permutations”) are possible?
5! = 120.
Permutations of {a, b, c, d, e}
These are the 5! = 120 ways of arranging 5 objects,
in such a way that all the different orders count as being distinct.
*******************************************
*********************************************************
NEGATIVE POWERS (EXPONENTS)
********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
*********************************************************
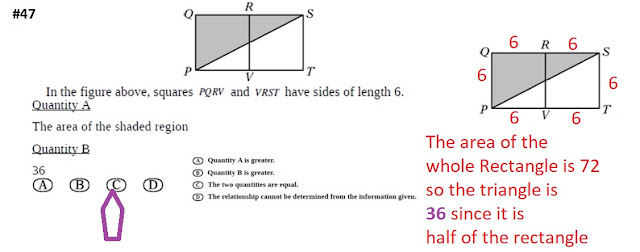
Everyone did well on #47
*********************************************************
*********************************************************
*********************************************************
*********************************************************
We probably need to talk about
FUNCTION NOTATION
VIDEO TO WATCH
BEFORE TRYING THE PROBLEM BELOW
LINK
*********************************************************
VIDEO LINK FOR #63
*********************************************************
*********************************************************
TWO VIDEOS for help with #71
******
******************************************************
**************************************************
**************************************************
**************************************************
**************************************************
**************************************************
**************************************************
**************************************************
**************************************************
**************************************************
*********
********************************************************************************
















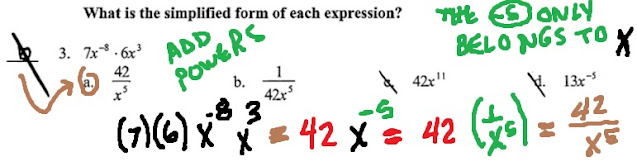










































































































No comments:
Post a Comment